在凝聚態物理學領域,量子摩爾材料研究正當時。本文將從一篇物理學版《馬說》講起,以期待讀者能夠欣賞該領域的新進展:得到更大晶格長度的 super-moiré 材料。我們將領略 super-moiré 材料所帶來的神奇物理效應,以及該研究如何完成從理論到計算再到實驗的完整閉環,實現前人開拓卻所不及的整數磁通布洛赫態和整數BZ振蕩,一窺其為量子世界研究開辟新路徑。
撰文 | 馬亞琪(香港科技大學)、黃美珍(香港科技大學)、卡洛、王寧(香港科技大學)
Super-moiré說
世有 moiré,然后有 super-moiré。Moiré 者常有,而super-moiré 不常有。
Moiré 之 super 者,其原胞尺度可達百納米,向之作者不知其能super 而制也。
是 super-moiré 也,其成于常規 moiré 之量子干涉效應,波粒二象性之力良有以也。
以百納米之原胞,所含磁通之量亦增百倍,Brown-Zak 振蕩正比于磁場之現象,昭然于世也。
噫!Brown-Zak,侯世達諸前輩得見今日之數據,其必曰“微斯人,吾誰與歸”矣。
題解
這段混搭了韓愈、范仲淹,還有幾位物理學家的《Super-moiré 說》,讓大家看得一頭霧水,先說一聲抱歉。但就是這樣文白夾雜古今中外的拉扯,其實包含著時下量子摩爾材料研究的新進展[1]。下面的文章,就好像諸位看官中學時學古文一樣,可以作為對此進展的賞析來讀。
量子摩爾材料(quantum moiré material)是指人造的二維超晶格材料,對于這類材料的理論、計算和實驗研究,是目前凝聚態物理學和量子材料科學的研究重點。其具體的例子包括雙層轉角石墨烯[2]和過渡金屬二硫化物。人們在前者中發現了超導現象,而目前正在世界范圍內如火如荼的分數陳絕緣體——庶幾分數量子霍爾效應的無磁場版本——就是在后者中發現的。這些材料的一個共同特點是,通過堆疊和旋轉,材料中形成的人造 moiré 晶格的尺度可以大于其單層組分中原子晶格的尺度,如單層的石墨烯中碳原子所形成的蜂窩晶格,其鍵長在埃米量級(10^(-10) m),而雙層轉角石墨烯的摩爾超晶格,其晶格長度可以到 10 納米(10^(-8) m)量級。在量子多體物理學和拓撲物理學中大家所追求的新奇現象,如二維(狄拉克)電子氣、莫特絕緣體、非費米液體、非常規超導體、量子反常霍爾效應(陳絕緣體)和其分數化的版本等等,都是因為這樣的長度尺度和能量尺度的變化而在量子摩爾材料中涌現出來,并且人們可以通過精準的門電壓、轉角、應變、垂直電場、外磁場等方式進行調控,在同一個樣品中實現這些新奇物態之間的相變,難怪摩爾材料變成了凝聚態物理學從理論到計算再到實驗,老少咸宜的熱門話題。
長度尺度和能量尺度的變化和隨之而來的新物理現象,能否在摩爾之上繼續進行呢?我們這里想要討論的進展,是在摩爾超晶格的基礎上,想辦法繼續增大超晶格原胞的尺度,把原胞從 10 納米(10^(-8) m)增大到了 100 納米(10^(-7) m)量級,這樣制造出來的二維超晶格材料,就是 Super-moiré[1]。
想要把原胞尺度變得更大,依靠人工堆疊兩種具有相似晶格常數的材料形成異質結是不可行的。異質結的原胞尺寸由這兩層二維材料間的晶格常數差所決定,而差是有限的。對于最常見的石墨烯(graphene)和六方氮化硼(hexagonal boron nitride,簡稱 hBN)形成的異質結,它的最大原胞尺度也才 ~14 納米。另一方面,簡單地調整同質結中兩層相同的二維材料之間的轉角也不能實現更大的原胞尺度(雖然之前有不少嘗試)。這是因為在實際材料中,原子排布的不均勻性是一個很大的問題,而且摩爾材料的雙層或者多層之間通過范德瓦爾斯力(而不是三維材料中常見的化學鍵)聯系在一起。范德瓦爾斯力不似化學鍵那么強,原子可以比較容易地調整位置找到局域基態,但從整體上看,這會使原子排布更加混亂,不能成為周期性的晶格。
那么如何克服這樣的問題呢?還是那句老話,“遇事不決,量子力學”。解決問題的辦法是把兩個已經穩定的 moiré 超晶格再疊加起來,并旋轉到合適的角度。當是時也,疊加在一起的穩定 moiré 超晶格(其原胞大小都在 10 納米左右),其中電子的波函數(波粒二象性)會發生干涉效應:如果兩個 moiré 之間相對的轉角滿足了干涉所需要的公度(commensurate)條件,也就是兩套 moiré 的倒格矢滿足特定關系時,兩個 moiré 的波長可以發生干涉,那么這樣干涉出來的波就可以具有更長的波長。如此產生的 super-moiré 超晶格,其晶格長度可以克服上面說的材料的不均勻性,展現出穩定的更大原胞的周期性晶格結構。正因為 super-moiré 的形成靠的是兩個穩定的 moiré 超晶格中電子波函數的量子力學干涉效應,而不是機械地通過旋轉讓原子密度簡單地在幾何上排列出更大的周期(遑論實際材料中原子排布天生不均勻,原子密度不能真正形成周期),所以說 “波粒二象性之力良有以也”。我們目前所得到的實驗結果,其實只是理論中滿足公度條件的諸多干涉波長中的一種,可以預期此路一開,還會有更多的 super-moiré 材料被制造出來,在更大長度尺度上的新奇量子多體物理學現象和拓撲物理學現象會不斷涌現。
那么有了更大晶格長度的 super-moiré,我們用它來展示什么新的物理現象呢?這就需要提到引言的《Super-moiré 說》中嵌入的幾位物理學家“Brown-Zak,侯世達諸前輩”和電子在晶格中的周期勢場和磁場的共同作用下,所展示的侯世達蝴蝶(Hofstadter butterfly)和 Brown-Zak 量子振蕩效應了。
侯世達的蝴蝶與 Brown-Zak 的振蕩
侯世達的蝴蝶(Hofstadter butterfly)不是混沌現象中經常提到的蝴蝶效應,侯世達也不是中國人,而是美國物理學家 D. R. Hofstadter(不得不說他的中文譯名很接地氣)。他在 1970 年代通過數值計算得到了在二維周期性勢場和垂直磁場中電子的量子運動的能譜圖,形如蝴蝶,故得名。他的結果也成為了現代科學計算數據可視化的早期范例之一[3]。

圖 1. 侯世達繪制的“蝴蝶圖”,描述二維正方形晶格中的電子的能級關于外加磁場的函數形式,形如蝴蝶。圖片來自文獻[4]。
二維正方形晶格中的電子的能級關于外加磁場的函數形式如圖 1 所示,該譜圖在數學結構上最顯著的特征是,在特定的磁場數值下(橫軸),電子可以處在的能量本征態(縱軸)可以隨著磁場的變化發生復雜的分裂,并產生迭代性的分形結構,形如蝴蝶。后面人們發現蝴蝶翅膀的特征是陳整數,所以侯世達蝴蝶在后來的整數量子霍爾效應理論和拓撲量子數理論中都有重要的作用。產生這樣圖案的實質原因是,在公度(commensurate)的條

場為零,可以擺脫磁場的束縛恢復自由的狀態,這樣在周期晶體中自由運動的電子的波函數,稱為布洛赫態(Bloch state),得名于瑞士物理學家 Felix Bloch(1905-1983),如圖 2.a 所示。侯世達蝴蝶能譜中的電子,在滿足磁場公度條件的時候,其波函數就是布洛赫態,其能量就是圖1 中有顏色的地方,此時電子可以傳導,考慮到此時有磁場(雖然電子在公度時感受不到),電子的波函數就被稱為磁布洛赫態;而在不滿足磁場的公度條件時,電子的波函數則處于絕緣態,其能量就是圖1 中空白的地方。
處在磁布洛赫態中的電子,因為不受磁場的束縛,可以保持彈道輸運,好像金屬中的自由電子在能帶中一樣(圖 2.c);如果調節磁場,把電子的狀態調節到圖 1 中空白的地方,此時電子就好像進入能帶中間的能隙而被約束,不能參與導電(圖 2.b)。如果可以測量侯世達蝴蝶(就是在二維周期性晶格勢場和垂直磁場中的電子)的輸運性質,并觀察其電導隨著磁場的關系,那么可以看到隨著磁場的變化,
穿過晶格原胞的磁通在“滿足—不滿足”公度條件的狀態之間變化;
電子的行為也就在對于磁場的“自由—約束”狀態之間變化;
其電導也就會出現隨著磁場“導電—不導電”的振蕩行為。
這樣的振蕩行為被稱為 Brown-Zak 振蕩(簡稱 BZ 振蕩),如圖 2. d, e, f 所示,得名于美國物理學家 Edmond Brown[5]和以色列物理學家 Joshua Zak[6]。這二位理論物理學家在 1960 年代就曾考慮過均勻磁場對于布洛赫電子運動的影響,可以說侯世達在 1970 年代的工作是建立在 Brown-Zak 的基礎之上的,只是 Brown-Zak 更多討論的是磁平移群的數學結構,而侯世達則把計算所得的蝴蝶能譜,還有能譜的分形結構挖掘了出來。

圖 2. 晶格原胞尺寸和磁場的公度條件及 BZ 振蕩。a. 沒有磁場時,電子在晶格勢場中自由運動,其波函數為布洛赫波。b. 有磁場但不滿足公度條件時,電子運動受到束縛。c. 滿足公度條件 /0 = /時,即穿過晶格原胞的磁通量為磁通量子的 / 倍,電子感受到的有效磁場為零,電子恢復磁布洛赫波的自由狀態。a,b,c, 來自文獻[8]。d. 當晶格原胞(灰色六邊形)較小時,需要多個原胞才能承載一個磁通量子。藍色六邊形表示在一定磁場強度下承載一個磁通量子需要的面積,灰色箭頭表示一個磁通量子。即一個晶格原胞只能穿過分數個磁通量子,也就是 /0 =1/( = 1,2,3, … ) 。那么實驗上可以看到隨 1/ 做周期性變化的分數 BZ 振蕩,如圖 e 所示。當晶格原胞變大時,在同樣的磁場下一個原胞(super-moire 原胞,紅色六邊形)能承載整數個磁通量子,即/0 = ( = 1,2,3, … )。那么實驗上可以看到隨 做周期性變化的整數 BZ 振蕩,如圖 f 所示。
行文至此都是理論和計算物理學家的游戲,在真實的二維材料中,能否觀察到侯世達蝴蝶和 BZ 振蕩呢?一如地球上的很多事情,理想和現實的差距就是那么大,那么不遂人意。這

要在真實的物理材料中觀察到 BZ 振蕩,需要盡量地增大晶格原胞的面積(就是原胞的尺寸),這樣才能在一個原胞中盡可能多地囊括磁通量子的 / 倍,才能看到系統的電導隨著磁場,以/ 為周期的 BZ 振蕩行為。圖 2. d, e, f 就是這樣現象的示意圖。
直到近些年,侯世達蝴蝶和 BZ 振蕩才在二維量子材料中被實現。2013 年,通過將 hBN 和石墨烯的晶軸對齊,英國曼徹斯特大學的 Fal'ko 和 Geim(2010 年諾貝爾物理學獎得主,因為發現石墨烯而聞名)得到了 Graphene/hBN(縮寫為 G/hBN)摩爾超晶格,其波長在 10 納米左右。這個數值比石墨烯的晶格常數大了將近 40 倍,意味著原胞面積增大

說,如 G/hBN 這樣的普通 moiré 材料中的原胞面積 仍然不夠大。只要把 增大,比如原胞的線性尺度從 10 納米增大到 100 納米,原胞的面積就可以再增大了 100 倍,所需要看到同樣 BZ 振蕩的磁場就可以減小 100 倍——這就是 super-moiré 材料發揮作用的地方。如前所述,我們的 super-moiré 提供了一種創造周期為幾十個納米的結構,這為研究侯世達能譜和整數 BZ 振蕩提供了一個良好的平臺。
世有 moiré,然后有 super-moiré
構建 super-moiré,就是要構建尺度為 ~100 納米的周期性勢場。正如前文中所提到的,在量子摩爾材料的構建方法中,異質結中原胞尺寸有限,小于需要的長度;大尺度周期性結構在極小轉角的同質結中是可能的,但是在現實中結構弛豫會導致嚴重的不均勻性。直到現在,整數磁通的 BZ 振蕩只在非常有限的系統中被實現。同時,在這些系統中,電荷捕獲中心(charge trap centers)、雜質、角度不均勻性和層間耦合引起的電子能帶變化都會阻礙整數磁通布洛赫態的實現。
我們的解決辦法,是通過兩個穩定的 moiré 超晶格的堆疊和旋轉,讓當兩套 moiré 的倒格矢滿足公度關系,此時電子波函數發生量子力學干涉效應,進而可以實現 super-moiré 的更大周期[1]。如圖 3.a 所示,通過把單層石墨烯和 1.0° 的轉角六方氮化硼(twisted hBN,簡稱 t-hBN)對齊,我們創造了兩個小尺度的摩爾結構:一個是 14.4 納米的 t-hBN moiré,另一個是 13.0 納米的 G/hBN moiré。這兩個摩爾結構會相互干涉從而形成一個 63.2 納米的 super-moiré 結構,在主狄拉克點(Main Dirac point,單層石墨烯的本征電阻峰,對應 tot = 0)附近出現的電阻峰證明了這一點 (圖 3.c)。如此構造簡潔干脆,卻效果顯著。通常使用的 hBN 晶體是自然堆疊的 AA’結構,通過小角度堆疊兩個奇數層的 hBN 晶 體,可以創造一個平行堆疊的界面。這樣的堆疊方式會在界面處產生第一個 t-hBN moiré 圖案(圖 3.a的右邊),其中對稱性破缺會產生一個周期性勢場[9]。這個勢場是靜電性的,并且可以在沒有直接接觸的情況下影響相鄰的材料。同時,當單層石墨烯進一步和t-hBN 對齊,石墨烯和 hBN 之間的晶格常數差可以產生第二個 G/hBN moiré 圖案(圖 3.a 的左邊)。在 t-hBN 和 G/hBN 界面處產生的勢場擁有不同的周期和幅度(示意圖如圖 3.b)。通過控制 G/hBN 和 t-hBN 中的轉角大小,這兩個摩爾結構可以產生量子干涉并形成 t-hBN/G/hBN super-moiré 結構(圖 3.a 的中間),這個新的摩爾結構通常具有比兩個單摩爾結構更大的周期尺度。這樣,在石墨烯中運動的電子會感受到一個大尺度的 super- moiré 勢場(圖 3.b)。

圖 3. Super-moiré 周期性勢場的產生。 a. 兩個單摩爾結構和 super-moiré 結構的示意圖;b. t-hBN 和 G/hBN勢場疊加的示意圖,以此產生大周期的 t-hBN/G/hBN 勢場;c. 縱向電阻隨載流子濃度的變化關系(T =1.5K)。數據來自文獻 [1]。


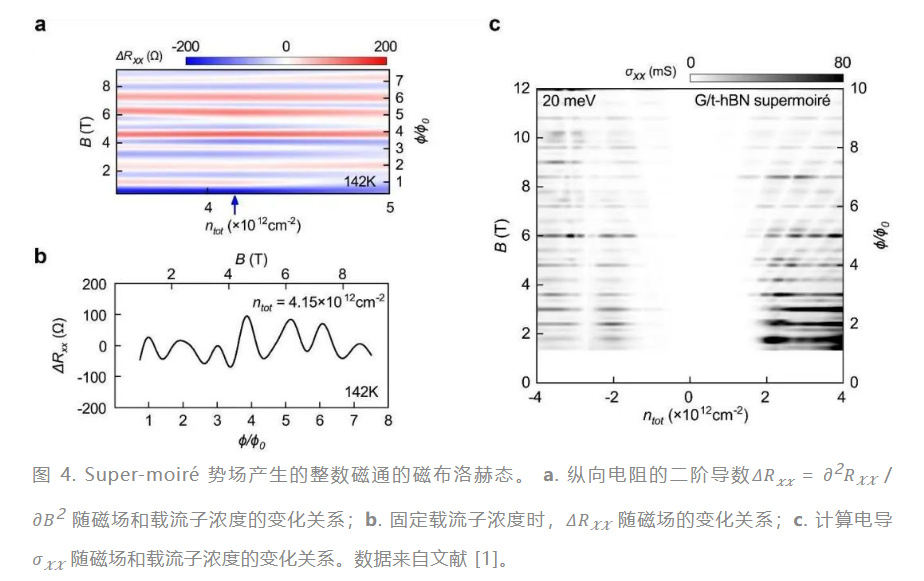
微 super-moiré,吾誰與歸

變化的量子 振蕩,即整數 BZ 振蕩,這項工作不僅為研究高磁通(/ > 1)下的侯世達蝴蝶能譜提供了機會,而且為創造均勻的大尺度超摩爾(super-moiré)周期性勢場提供了新的方法。從 1960 年代的 Brown-Zak,到 1970 年代的侯世達,到 graphene 和 moiré 時代的 Fal’ko 和 Geim,再到今天的 super-moiré,二維周期性勢場和垂直磁場中電子的量子運動的故事,從理論到計算再到實驗,終于在地球上實驗室里面畫了一個完整的圈。所以說如果 Brown-Zak,侯世達諸位前輩看到當下的進展,“其必曰:微斯人,吾誰與歸?”
當然,在我們之前,其他人也探索了類似的現象。比如堆疊兩個 hBN/G 界面形成 hBN/G/hBN 結構[11],或者堆疊兩個 G/G 界面形成三層轉角石墨烯結構[12]。這兩個結構的共同點是使用相同類型的 moiré 堆疊,通過相鄰層之間的近鄰耦合(proximity coupling)形成 super-moiré。但這種設計有兩個缺點:首先,相鄰層之間距離固定導致勢場強度無法調節;此外,由于近鄰耦合要求不同層材料在空間上不能離太遠,因此想要疊加更多層結構來制造更復雜的 super-moiré 幾乎不可能。
不同的是,我們所采用的 t-hBN/G/hBN super-moiré 結構由不同類型的moiré 組成,避開了上面兩個缺點。這是因為 G/t-hBN 中 t-hBN 的勢場來自于界面處電極化產生的靜電勢,這種勢場允許不同層材料在空間上的分離,并且可以通過變化 hBN 厚度來調節勢場強度。此外,hBN 作為一個絕緣體,不直接參與電子輸運,相對于三層轉角石墨烯這種電子性質被層間相互作用強烈改變的系統,G/t-hBN super-moiré 結構是一個相對干凈的系統。這種通過量子力學干涉效應制造的 super-moiré 器件,將有望實現清晰可控的高密度單光子源陣列、三維拓撲絕緣體[13]等,將會在量子通信和量子計算等領域具有重要應用前景。
參考文獻
[1]. Ma, Y., Huang, M., Zhang, X., Hu, W., Zhou, Z., Feng, K., Li, W., Chen, Y., Lou, C., Zhang, W, Ji, H., Wang, Y., Wu, Z., Cui, X., Yao, W., Yan, S., Meng, Z. Y. & Wang, N. Magnetic Bloch States at Integer Flux Quanta Induced by Super-moiré Potential in Graphene Aligned with Twisted Boron Nitride. Nature Communications 16, 1860 (2025).
[2]. 轉角石墨烯的三昧|量子多體中的吶喊與彷徨之九, 返樸.
[3]. Hofstadter, D. R. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Physical Review B 14, 2239 (1976).
[4]. Harper, F., Simon, S. H. & Roy, R. Perturbative approach to flat Chern bands in the Hofstadter model. Physical Review B 90, 075104 (2014).
[5]. Brown, E. Bloch electrons in a uniform magnetic field. Physical Review 133, A1038 (1964).
[6]. Zak, J. Magnetic translation group. Physical Review 134, A1602 (1964).
[7]. Ponomarenko, L., Gorbachev, R., Yu, G., Elias, D., Jalil, R., Patel, A., Mishchenko, A., Mayorov, A., Woods, C., Wallbank, J., Mucha-Kruczynski, M., Piot, B., Potemski, M., Grigorieva, I., Novoselov, K., Guinea, F., Fal’ko, V. & Geim, A. Cloning of Dirac fermions in graphene superlattices. Nature 497, 594-597 (2013).
[8]. Krishna Kumar, R., Mishchenko, A., Chen, X., Pezzini, S., Auton, G., Ponomarenko, L., Zeitler, U., Eaves, L., Fal’ko, V. & Geim, A. High-order fractal states in graphene superlattices. Proceedings of the National Academy of Sciences 115, 5135-5139 (2018).
[9]. Zhao, P., Xiao, C. & Yao, W. Universal superlattice potential for 2D materials from twisted interface inside h-BN substrate. npj 2D Materials and Applications 5, 38 (2021).
[10]. Krishna Kumar, R., Chen, X., Auton, G., Mishchenko, A., Bandurin, D. A., Morozov, S. V., Cao, Y., Khestanova, E., Ben Shalom, M., Kretinin, A., Novoselov, K., Eaves, L., Grigorieva, I., Ponomarenko, L., Fal’ko, V. & Geim, A. High-temperature quantum oscillations caused by recurring Bloch states in graphene superlattices. Science 357, 181-184 (2017).
[11]. Wang, L., Zihlmann, S., Liu, M.-H., Makk, P., Watanabe, K., Taniguchi, T., Baumgartner, A. & Schonenberger, New generation of moiré superlattices in doubly aligned hBN/graphene/hBN heterostructures. Nano letters 19, 2371-2376 (2019).
[12]. Zhu, Z., Carr, S., Massatt, D., Luskin, M. & Kaxiras, E. Twisted trilayer graphene: A precisely tunable platform for correlated electrons. Physical Review Letters 125, 116404 (2020).
[13]. Herzog-Arbeitman, J., Song, Z.-D., Regnault, N. & Bernevig, B. A. Hofstadter topology: noncrystalline topological materials at high flux. Physical Review Letters 125, 236804 (2020).

特 別 提 示
1. 進入『返樸』微信公眾號底部菜單“精品專欄“,可查閱不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關注公眾號,回復四位數組成的年份+月份,如“1903”,可獲取2019年3月的文章索引,以此類推。
版權說明:歡迎個人轉發,任何形式的媒體或機構未經授權,不得轉載和摘編。轉載授權請在「返樸」微信公眾號內聯系后臺。
上一篇:國際北極熊日|在極寒之地,這些“白色奇跡”如何成就王者之路?
下一篇:返回列表
【免責聲明】本文轉載自網絡,與科技網無關。科技網站對文中陳述、觀點判斷保持中立,不對所包含內容的準確性、可靠性或完整性提供任何明示或暗示的保證。請讀者僅作參考,并請自行承擔全部責任。

